|
Lei Lai I am a fourth-year PhD student in the Department of Computer Science at Boston University (BU), advised by Prof. Eshed Ohn-Bar. My research spans various areas, focusing on machine intelligence and computer vision, especially in their application to autonomous driving systems. Before joining Prof. Eshed Ohn-Bar's group, I worked on prize-collecting Steiner tree (PCST) project with Prof. Alina Ene (2020-2022). Prior to BU, I worked with Prof. Dingzhu Du as a research assistant, focusing on submodular function maximization problem (2019-2020). I received my master's degree in the Department of Mathematics at East China Normal University (ECNU), under the supervision of Prof. Changhong Lu, with a focus on Combinatorics and Graph Theory (2017-2020). |

|
Research |
|
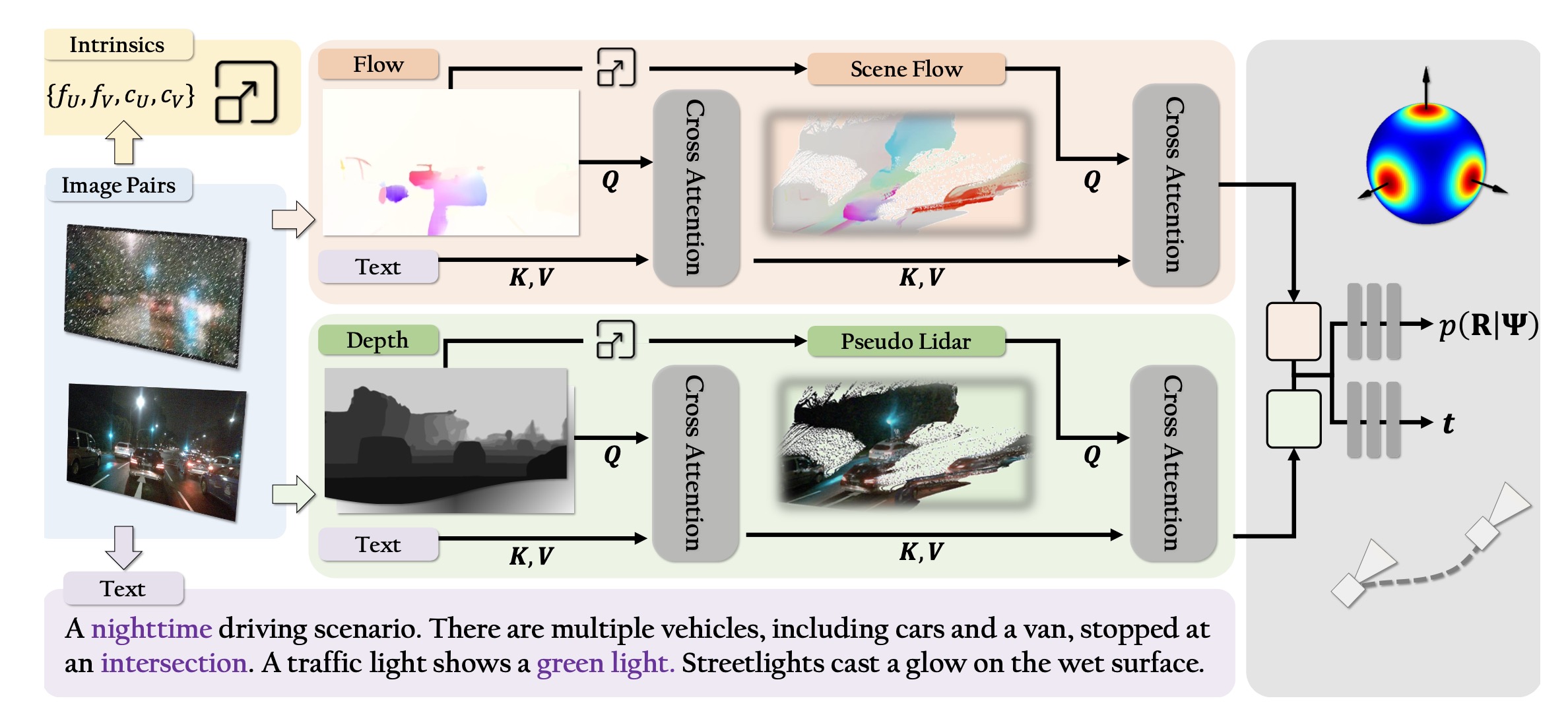
ZeroVO: Visual Odometry with Minimal Assumptions
Lei Lai*, Zekai Yin*, Eshed Ohn-Bar Conference on Computer Vision and Pattern Recognition (CVPR), 2025 project page / paper We introduce ZeroVO, a novel visual odometry (VO) algorithm that achieves zero-shot generalization across diverse cameras and environments, overcoming limitations in existing methods that depend on predefined or static camera calibration setups. Our approach introduces three core innovations: a calibration-free, geometry-aware network robust to noisy depth and camera estimates; a language-based prior for improved semantic understanding and generalization; and a semi-supervised training paradigm that adapts to new scenes using unlabeled data. We analyze complex driving scenarios, achieving over 30% improvement over prior methods on multiple real and synthetic benchmarks. By not requiring fine-tuning or camera calibration, our work broadens the applicability of VO, providing a versatile solution for real-world deployment at scale. |

|
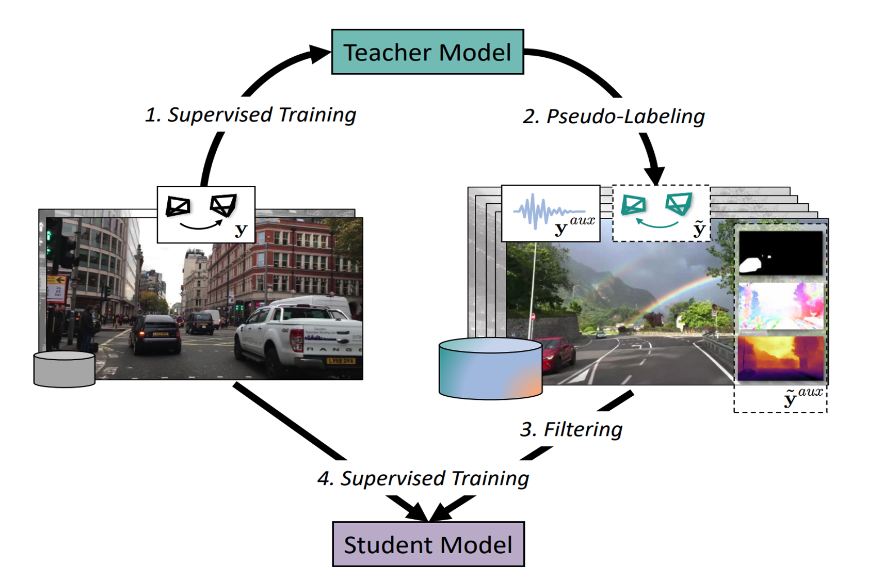
Uncertainty-Guided Never-Ending Learning to Drive
Lei Lai, Eshed Ohn-Bar, Sanjay Arora, John Seon Keun Yi Conference on Computer Vision and Pattern Recognition (CVPR), 2024 project page / paper We present a highly scalable self-training framework for incrementally adapting vision-based end-to-end autonomous driving policies in a semi-supervised manner, i.e., over a continual stream of incoming video data. To facilitate large-scale model training (e.g., open web or unlabeled data), we do not assume access to ground-truth labels and instead estimate pseudo-label policy targets for each video. Our framework comprises three key components: knowledge distillation, a sample purification module, and an exploration and knowledge retention mechanism. Trained as a complete never-ending learning system, we demonstrate state-of-the-art performance on training from domain-changing data as well as millions of images from the open web. |
|
XVO: Generalized Visual Odometry via Cross-Modal Self-Training
Lei Lai*, Zhongkai Shangguan*, Jimuyang Zhang, Eshed Ohn-Bar International Conference on Computer Vision (ICCV), 2023 project page / paper We propose XVO, a semi-supervised learning method for training generalized monocular Visual Odometry (VO) models with robust off-the-shelf operation across diverse datasets and settings. We empirically demonstrate the benefits of semi-supervised training for learning a general-purpose direct VO regression network, alongside the benefits of multi-modal supervision to facilitate generalized representations for the VO task. Combined with the proposed semi-supervised step, XVO demonstrates off-the-shelf knowledge transfer across diverse conditions on KITTI, nuScenes, and Argoverse without fine-tuning. |

|
Monotone submodular maximization over the bounded integer lattice with cardinality constraints
Lei Lai, Qiufen Ni, Changhong Lu, Chuanhe Huang, Weili Wu Discrete Mathematics, Algorithms and Applications (DMAA), 2019 paper We consider the problem of maximizing monotone submodular function over the bounded integer lattice with a cardinality constraint. We propose a random greedy \( (1-\frac{1}{e}) \)-approximation algorithm and a deterministic \( \frac{1}{e} \)-approximation algorithm. Both algorithms work in value oracle model. In the random greedy algorithm, we assume the monotone submodular function satisfies diminishing return property, which is not an equivalent definition of submodularity on integer lattice. Additionally, our random greedy algorithm makes \( \mathcal{O}((|\mathbb{E}|+1)\cdot k) \) value oracle queries and deterministic algorithm makes \( \mathcal{O}(|\mathbb{E}|\cdot B\cdot k^3) \) value oracle queries. |
Teaching
|
ServiceReviewer
|
Miscellanea
|